Feature Extraction
Overview
ratsgo’s speech book 를 보고 재작성
Fourier Transform
푸리에 변환(Fourier Transform)은 시간과 주파수 도메인 관련 함수를 이어주는 수학적인 연산
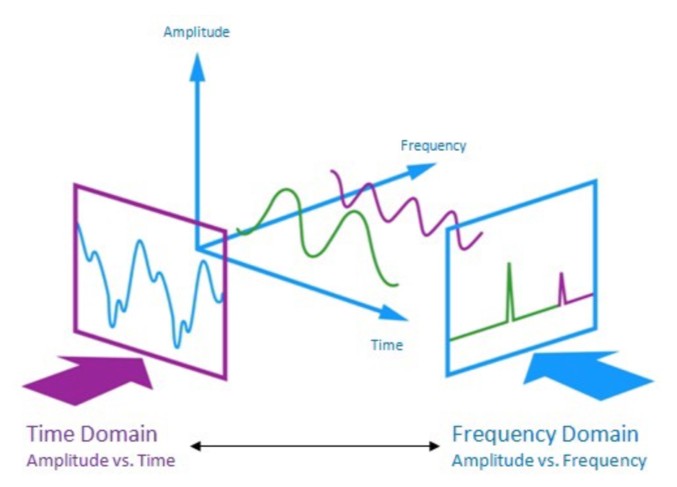
Discrete Fourier Transform
시간(time)에 대한 함수(혹은 신호)와 주파수(frequency)에 대한 함수(혹은 신호)를 잇는다.
- 이산 푸리에 변환(DFT)은 시간 도메인의 이산 신호를 주파수 도메인의 이산 신호로 변환하는 과정.
- 컴퓨터는 이산 데이터를 처리하는 데 적합하기 때문에 음성 인식과 같은 디지털 신호 처리 분야에서 DFT가 널리 사용 됨.
- 이산 푸리에 변환의 결과로 얻어진 주파수 도메인 신호를 다시 시간 도메인으로 변환하는 것을 이산 역푸리에 변환(IDFT)이라고 함.
- DFT와 IDFT는 수학적으로 비슷하지만, 지수 함수 내의 부호 차이로 구분. DFT는 음수의 지수를 사용하고, IDFT는 양수의 지수를 사용.
DISCRETE FOURIER TRANSFORM
\[X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i \frac{2\pi k n}{N}}\]INVERSE DISCRETE FOURIER TRANSFORM
\[X_k = \sum_{n=0}^{N-1} x_n \cdot e^{i \frac{2\pi k n}{N}}\]Concepts
오일러 공식(Euler’s formula)
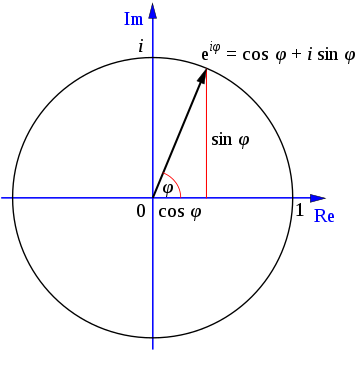
\[e^{i\theta} = \cos\theta + i\sin\theta\]허수 단위 i는 제곱하면 -1이 되며, θ에 π를 대입하면 오일러의 등식 exp(iπ) + 1 = 0을 얻는다.
복소 평면에서 exp(iθ)는 반지름이 1인 단위원을 그리며, 실수부는 cosθ, 허수부는 isinθ로 표현.
xn 은 시간 도메인의 n번째 샘플, Xk는 주파수 도메인의 k번째 푸리에 변환 결과물 k/N 은 주파수
식을 봤을 때 전체 복소평면상 이들 점들을 모두 더하는 것이므로 시간 도메인의 원래 신호의 무게 중심이라고 볼 수 있다.
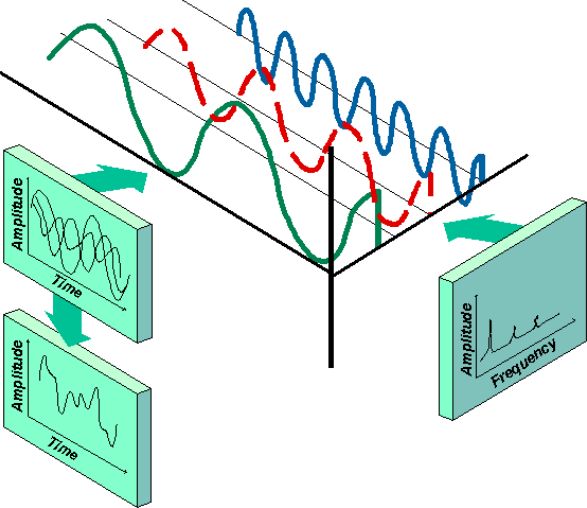
즉 변환을 하게 되면 k/N 을 x축 Xk y로 하는 주파수에 대한 값으로 변환이 된다.
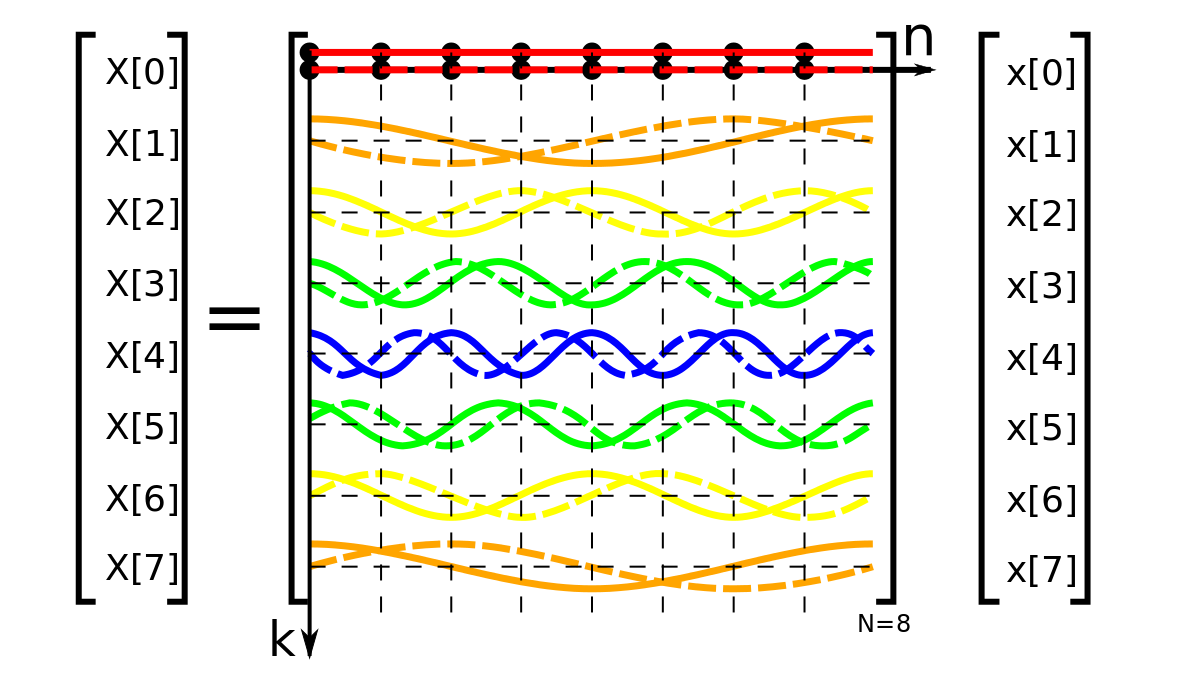
DFT Matrix
matrix form 으로 나타냄.
- 벡터 x 는 시간 도메인의 원래 신호,
- 행렬 W는 exp 항
- W 는 N×N 크기로 행 인덱스는 k 열 인덱스는 n
- W 의 각 행은 복소평면상 단위원에서 도는 각기 다른 각 속도
이산 푸리에 변환의 본질은 선형 변환(linear transform)
DFT 행렬은 켤레 전치가 역행렬(inverse matrix)와 같은 복소수 행렬, 즉 유니타리 행렬(unitary matrix).
아래는 Python Code 예시
import numpy as np
def DFT(x):
x = np.asarray(x, dtype=float)
N = x.shape[0]
n = np.arange(N)
k = n.reshape((N, 1))
W = np.exp(-2j * np.pi * k * n / N)
return np.dot(W, x)
MFCCs
Mel-Frequency Cepstral Coefficients(MFCC)는 음성 인식과 관련해 불필요한 정보는 버리고 중요한 특질만 남긴 피처(feature)이다.
deterministic 한 추출 방법
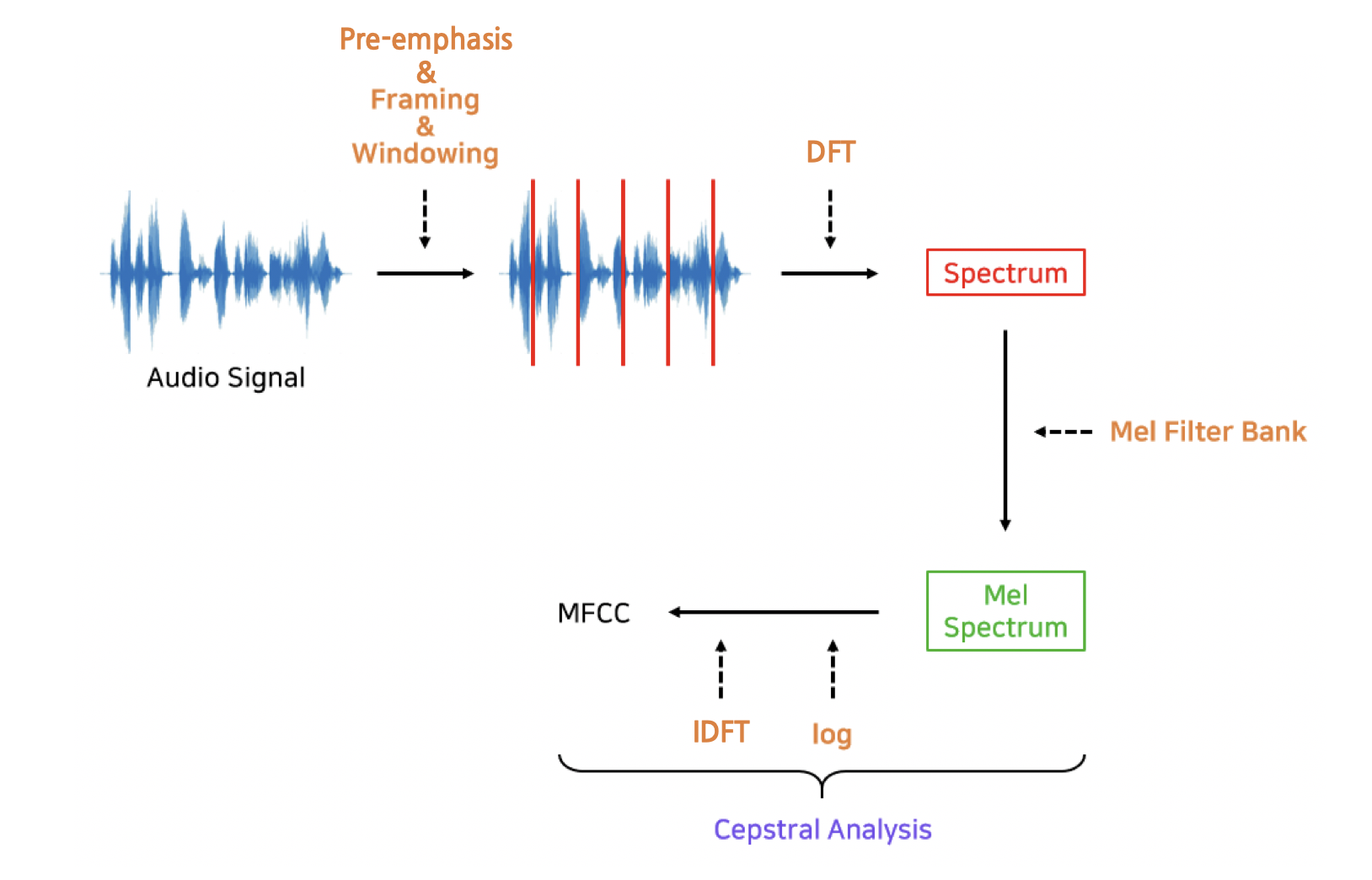
- Frame : 대개 25ms 내외로 잘게 만든 것.
- spectrum : 프레임 각각에 푸리에 변환(Fourier Transform)을 실시해 해당 구간 음성(frame)에 담긴 주파수(frequency) 정보를 추출
- Mel Filter Bank : 스펙트럼에 사람의 말소리 인식에 민감한 주파수 영역대는 세밀하게 보고 나머지 영역대는 상대적으로 덜 촘촘히 분석하는 필터
- log-Mel Spectrum : 로그를 취한 것
- MFCC: log-Mel Spectrum 에 역푸리에변환(Inverse Fourier Transform)을 적용해 주파수 도메인의 정보를 새로운 시간(time) 도메인으로 바꾼 것
- MFCC는 기존 음성 인식 시스템에서 가우시안 믹스처 모델(Gaussian Mixture Model)의 입력으로 쓰임
import scipy.io.wavfile
sample_rate, signal = scipy.io.wavfile.read('example.wav')
>>> sample_rate
16000
>>> signal
array([36, 37, 60, ..., 7, 9, 8], dtype=int16)
>>> len(signal)
183280
>>> len(signal) / sample_rate
11.455
signal = signal[0:int(3.5 * sample_rate)]
Preemphasis
고주파 성분의 에너지를 올려주는 전처리 과정
- 상대적으로 에너지가 적은 고주파 성분을 강화함으로써 원시 음성 신호가 전체 주파수 영역대에서 비교적 고른 에너지 분포를 갖도록 함.
- 푸리에 변환시 발생할 수 있는 numerical problem 예방.
- Signal-to-Noise Ratio(SNR) 개선.
first-order high-pass filter 라고 하며 수식은 아래와 같다.
\[y_t = x_t - \alpha x_{t-1}\]즉, 고역을 약하게 하는 방법
α 는 보통 0.95나 0.97을 사용
Framing
- MFCC 생성 과정에서는 변화가 빠른 원시 음성 신호를 분석하기 위해 푸리에 변환을 사용하여 주파수 정보를 추출.
- 음성 신호가 시간에 따라 일정하다고 가정할 수 있는 짧은 시간 단위로 신호를 쪼개는 과정을 ‘framing’이라 하며, 일반적으로 25ms 길이로 진행.
- Framing 시에는 프레임들이 일부 겹치도록 하여(frame_stride=10ms), 연속성을 유지하고 정보 손실을 방지.
frame_size = 0.025
frame_stride = 0.01
frame_length, frame_step = frame_size * sample_rate, frame_stride * sample_rate
signal_length = len(emphasized_signal)
frame_length = int(round(frame_length))
frame_step = int(round(frame_step))
# frame_step만큼 이동시키면서 몇 개의 프레임으로 나눌 수 있는지 계산. np.ceil은 나눗셈의 결과가 소수점이 나오면 올림하여 프레임 수가 부족하지 않게 함
num_frames = int(np.ceil(float(np.abs(signal_length - frame_length)) / frame_step))
# 패딩은 마지막 프레임이 frame_length만큼의 데이터를 갖도록 하기 위해 추가
pad_signal_length = num_frames * frame_step + frame_length
# 필요한 길이만큼 0으로 채운 배열을 생성하고, np.append를 사용하여 원본 신호 끝에 추가
z = np.zeros((pad_signal_length - signal_length))
pad_signal = np.append(emphasized_signal, z)
# 배열을 반복하여 타일처럼 확장 각 인덱스 추출
# 인덱스 범위가 0~399인데 두번째 프레임에 관련된 범위는 160~559임을 확인할 수 있다. 이전 프레임과 다음 프레임이 서로 겹친다
indices = np.tile(np.arange(0, frame_length), (num_frames, 1)) + \
np.tile(np.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T
frames = pad_signal[indices.astype(np.int32, copy=False)]
원시 음성을 짧은 구간(25ms)으로 자르되 일부 구간(10ms)은 겹치게 처리한 것
Windowing
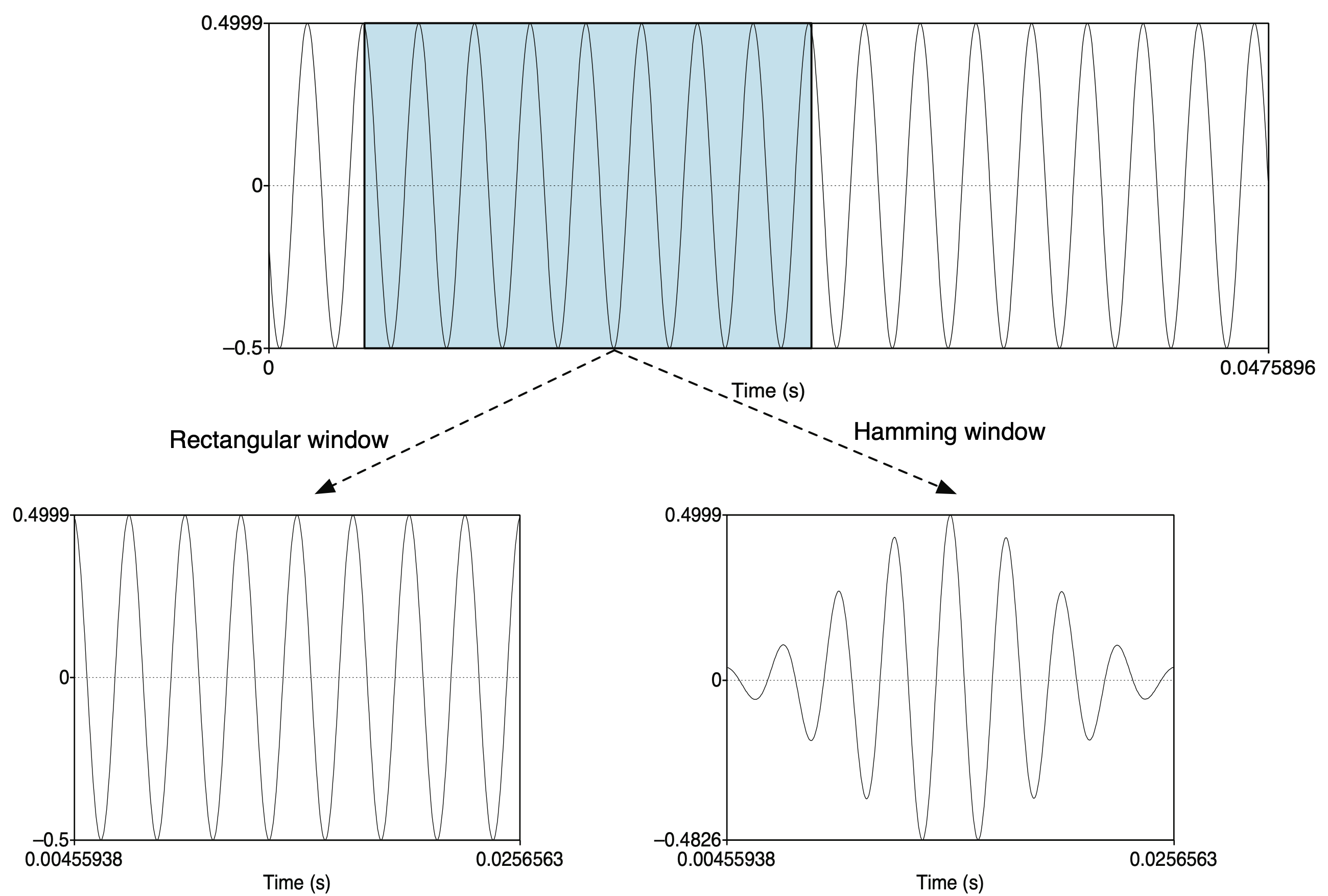
- Windowing은 프레임에 특정 함수를 적용하여 경계를 부드럽게 만드는 기법.
- 해밍 윈도우는 이러한 함수 중 하나로, 중간은 원래 신호를 유지하고 양 끝을 감소시켜 신호의 급격한 변화를 완화.
- 프레임의 양 끝에서 신호가 갑자기 0이 되는 것을 방지하고, 푸리에 변환 시 발생할 수 있는 불필요한 고주파 성분을 줄여주어, 변환된 신호의 품질을 향상.
Magnitude
- MFCC를 구할 때는 음성 인식에 불필요한 위상 정보는 없애고 진폭 정보만을 남긴다.
- 진폭(magnitude) : 이 주파수 성분의 크기
- 위상(phase): 위상은 해당 주파수의 (복소평면상 단위원상)위치
복소수 입력(a+b×j)에 대해 √a2+b2 를 리턴
mag_frames = np.absolute(dft_frames)
Power Spectrum
복소수 형태인 이산 푸리에 변환 결과를 모두 실수(real number)로 바꿈
\[\text{Power} = \frac{|X[k]|^2}{N}\]pow_frames = ((1.0 / NFFT) * ((mag_frames) ** 2))
Filter Banks
저주파수 영역대를 고주파수 영역대 대비 상대적으로 세밀하게 볼 필요가 있어 적용하는 기법

헤르츠 기준 저주파수 영역대를 세밀하게 살피고, 고주파수 영역대를 넓게 보는 필터
nfilt = 40
low_freq_mel = 0
high_freq_mel = (2595 * np.log10(1 + (sample_rate / 2) / 700)) # Convert Hz to Mel
mel_points = np.linspace(low_freq_mel, high_freq_mel, nfilt + 2) # Equally spaced in Mel scale
hz_points = (700 * (10**(mel_points / 2595) - 1)) # Convert Mel to Hz
bin = np.floor((NFFT + 1) * hz_points / sample_rate)
fbank = np.zeros((nfilt, int(np.floor(NFFT / 2 + 1))))
for m in range(1, nfilt + 1):
f_m_minus = int(bin[m - 1]) # left
f_m = int(bin[m]) # center
f_m_plus = int(bin[m + 1]) # right
for k in range(f_m_minus, f_m):
fbank[m - 1, k] = (k - bin[m - 1]) / (bin[m] - bin[m - 1])
for k in range(f_m, f_m_plus):
fbank[m - 1, k] = (bin[m + 1] - k) / (bin[m + 1] - bin[m])
>>> len(fbank[0])
257
>>> len(fbank[39])
257
>>> fbank[0]
array([0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0.])
>>> fbank[39]
array([0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.06666667, 0.13333333, 0.2 , 0.26666667, 0.33333333,
0.4 , 0.46666667, 0.53333333, 0.6 , 0.66666667,
0.73333333, 0.8 , 0.86666667, 0.93333333, 1. ,
0.94117647, 0.88235294, 0.82352941, 0.76470588, 0.70588235,
0.64705882, 0.58823529, 0.52941176, 0.47058824, 0.41176471,
0.35294118, 0.29411765, 0.23529412, 0.17647059, 0.11764706,
0.05882353, 0. ])
filter[0] 은 내적을 통해 저주파 영역을 세밀하게 보고, filter[39] 는 고주파 영역을 넓게 본다.
filter_banks = np.dot(pow_frames, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks) # Numerical Stability
Log-Mel Spectrum
사람의 소리 인식은 로그(log) 스케일에 가까움.
사람이 두 배 큰 소리라고 인식하려면 실제로는 에너지가 100배 큰 소리여야 한다.
따라서 멜 스펙트럼에 로그 변환을 수행.
filter_banks = 20 * np.log10(filter_banks) # dB
MFCCs
변수 간 독립(independence)을 가정하고 모델링하는 가우시안 믹스처 모델(Gaussian Mixture Model)에 독립적이지 않은 피쳐는 적합하지 않다.
멜 스펙트럼과 같이 푸리에 변환으로 도메인간의 상관관계를 갖고 있는 경우 적합하지 않으므로, 역푸리에 변환(Inverse Fourier Transform)을 수행해 변수 간 상관관계를 해소한다.
이를 Mel-frequency Cepstral Coefficients(MFCCs) 이라 한다.
주파수 도메인 정보가 새로운 도메인으로 바뀌어 이전 대비 상대적으로 변수 간 상관관계가 해소 됨.
역이산 코사인 변환(Inverse Discrete Cosine Transform)을 사용하고 코사인 변환은 푸리에 변환에서 실수 파트만을 수행한다.
from scipy.fftpack import dct
num_ceps = 12
mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1 : (num_ceps + 1)] # Keep 2-13
버리는 정보가 많기 때문에 최근 딥러닝 기반 모델들에서는 MFCCs보다는 멜 스펙트럼 혹은 로그 멜 스펙트럼 등이 더 널리 쓰인다.
Post Processing
MFCCs를 입력으로 하는 음성 인식 시스템의 성능을 높이기 위해 하는 후처리.
Lift, Mean Normalization 등이 있다. 전자는 MFCCs에, 후자는 멜 스펙트럼 혹은 로그 멜 스펙트럼에 실시


Comments