Hidden Markov Chain

Hidden Markov Chain

Intro

stanford asr-introduction 과 ratsgo’s HMM 을 보고 재작성

Markov Model

\[P(X_{n} = j | X_{n-1} = i, X_{n-2} = i_{n-2}, ..., X_0 = i_0) = P(X_{n} = j | X_{n-1} = i)\]

(X_k)는 시간 (k)에서의 상태.

Output-independence를 가정한다

\[P(o_t | O_{1}^{t-1}, q_{1}^{t}) = P(o_t | q_t)\]

현재 상태가 오직 바로 이전의 과거 상태에만 의존하고 더 과거의 상태나 어떻게 현재 상태에 도달했는지에 대한 정보에는 의존하지 않는 모델

과거의 역사보다는 현재 상태가 미래의 상태를 결정하는 데 더 중요하다는 가정을 기반으로 함.

Markov Chain

Markov chain = First-order observable Markov Model

특정 시점 t에서의 State는 바로 이전 시점 t-1에서의 State의 영향을 받는다는 의미

마코브 체인은 마코브 특성을 갖고 이산적인 시간 흐름에 따른 시스템의 상태 변화를 확률적으로 나타낸 이산확률과정(또는 Discrete Markov Process)이다.

FSM(Finite State Machine)처럼 특정 시점 t에 대한 State가 존재하며, 시간의 진행에 따라 특정 State에서 다른 State로 Transition을 한다

\(Q = \{q_1, q_2, \ldots, q_N\}; \text{ the state at time } t \text{ is } q_t\) Q 는 각 시간 별 state 를 의미한다.

아래 식은 스테이트를 변환하는 전이 행렬이 된다. \(a_{ij} = P(q_t = j \mid q_{t-1} = i) \quad 1 \leq i, j \leq N \\ \sum_{j=1}^{N} a_{ij} = 1; \quad 1 \leq i \leq N\)

Example

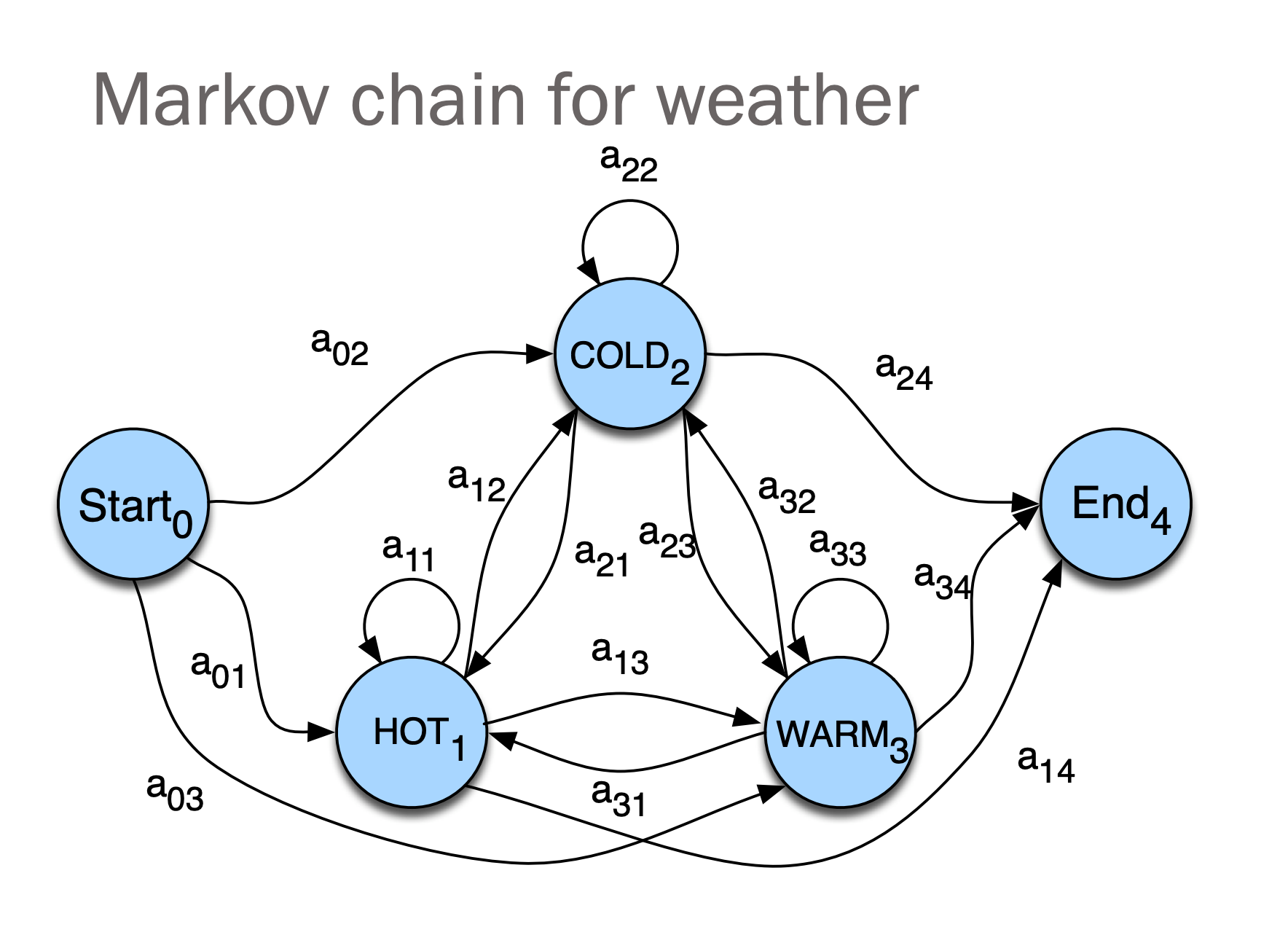
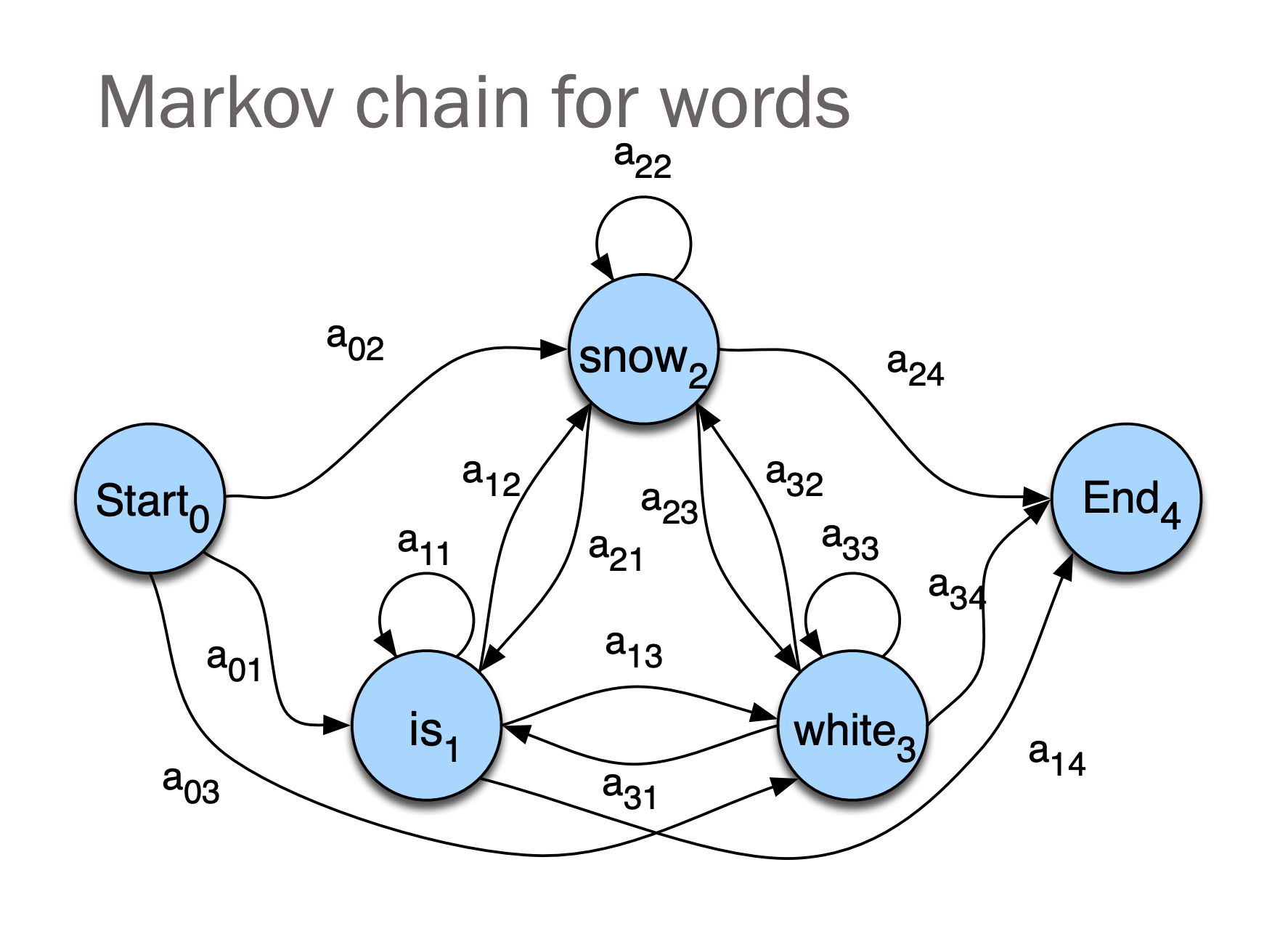
Start state

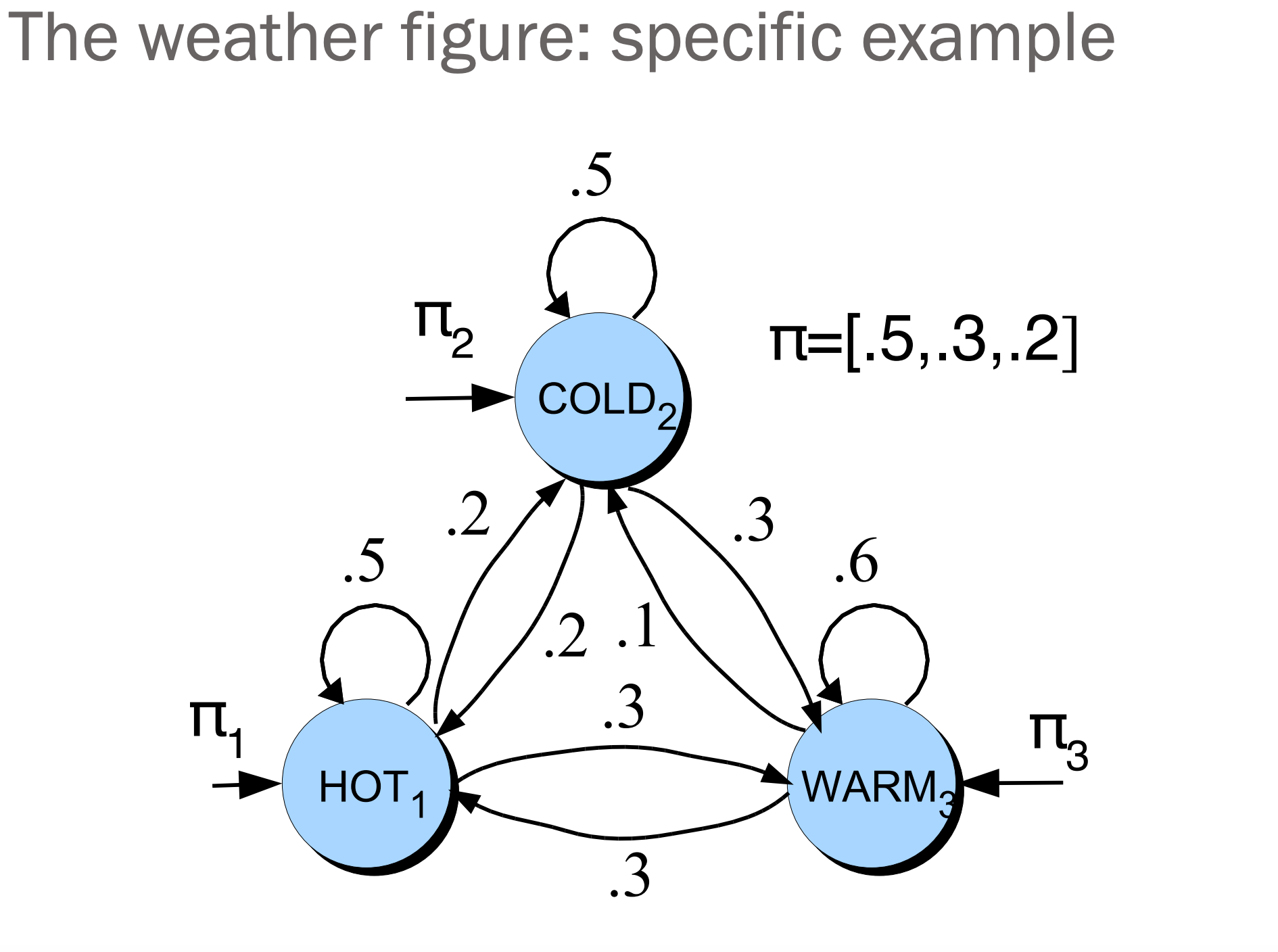
시작 상태 역시 확률로 표현하여 표현한다.

\[[ \pi_i = P(q_1 = i) \quad 1 \leq i \leq N ] [ \sum_{i=1}^{N} \pi_i = 1 ]\]

Problem

기존 마코브 체인에서는 출력 심볼이 상태 심볼과 같다.

예를 들어, 더운 날씨를 보면 우리는 ‘더운’ 상태에 있다고 할 수 있음.

하지만 음성 인식에서는 출력 심볼은 음향 벡터(Cepstrum: 푸리에 변환한 특징), 숨겨진 상태는 ‘phones’(음소)이다.

그래서 마코브 체인을 그대로 사용하지 못한다. 그래서 입력 심볼과 상태가 같지 않은 마코브 체인의 확장인

히든 마코브 모델(Hidden Markov Model)을 사용한다.

우리가 어떤 상태에 있는지 알 수 없다는 것을 의미.

Hidden Markov Chain

관측치 뒤에 은닉되어 있는 상태(state)를 추정하고자 할 때 사용

\[P(q_i | q_1, \ldots, q_{i-1}) = P(q_i | q_{i-1})\]

Hidden Markov Chain Case

아래는 대표적인 HMM이 사용되는 케이스

• 당신은 2799년의 기후학자입니다.
• 지구 온난화를 연구하고 있습니다.
• 2008년 여름, 메릴랜드주 볼티모어의 날씨 기록을 찾을 수 없습니다.
• 하지만 제이슨 아이스너의 일기를 발견했습니다.
• 그 일기에는 그 여름, 제이슨이 매일 몇 개의 아이스크림을 먹었는지가 기록되어 있습니다.
• 우리의 임무: 그 여름 얼마나 더웠는지 알아내는 것입니다.

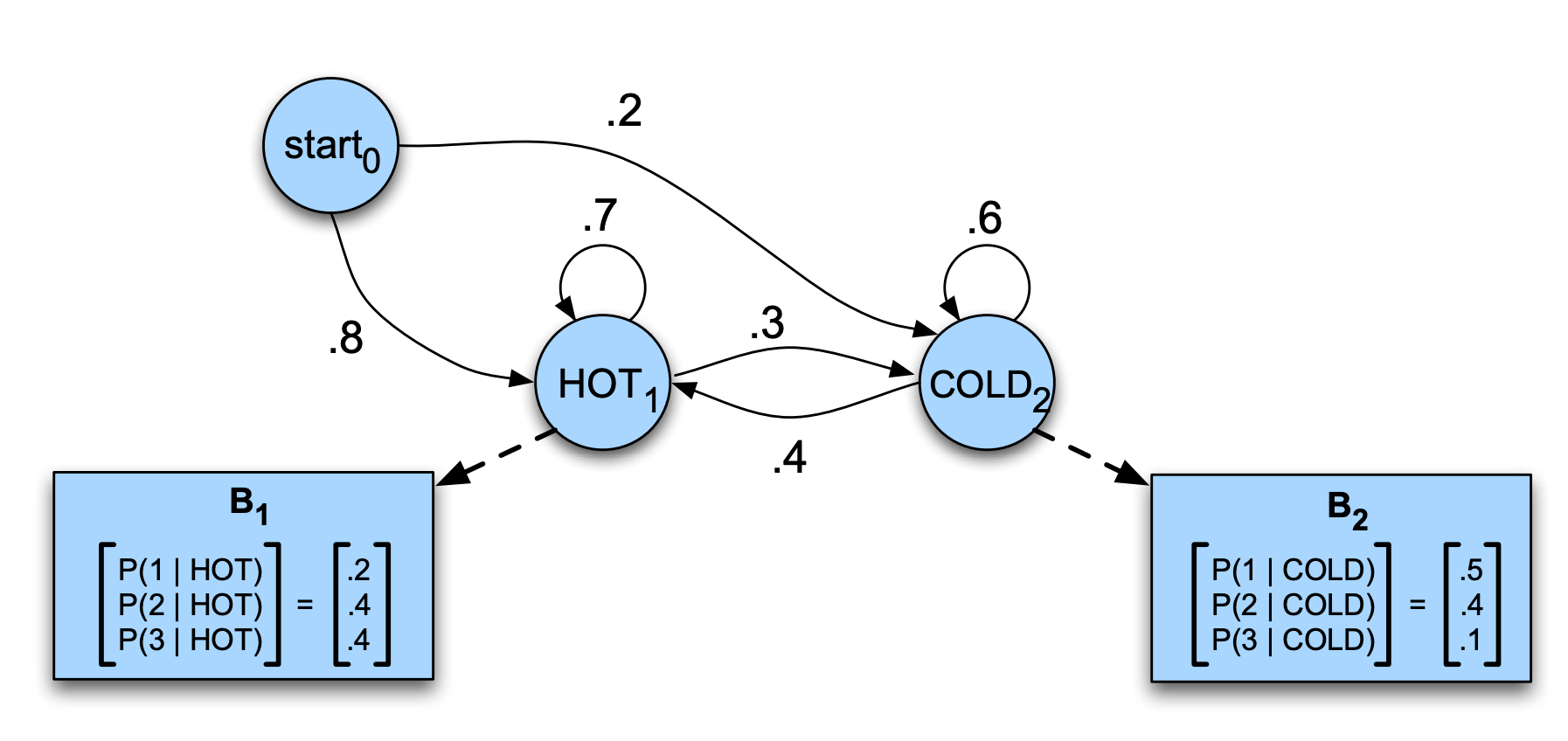
𝐵는 방출확률(emission probablity, likly hood), 은닉된 상태로부터 관측치가 튀어나올 확률이라는 의미

\[P(3 1 3, \text{hot hot cold}) = P(\text{hot} | \text{start}) \times P(\text{hot} | \text{hot}) \times P(\text{cold} | \text{hot}) \times P(3 | \text{hot}) \times P(1 | \text{hot}) \times P(3 | \text{cold}) = 0.8 \times 0.6 \times 0.3 \times 0.4 \times 0.2 \times 0.1\]

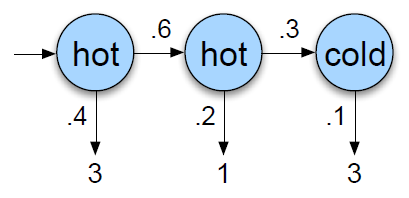
The Three Basic Problems for HMMs

1. Evaluation: 관측 시퀀스 O=(o1o2…oT)와 HMM 모델 F = (A,B)가 주어졌을 때, 모델을 고려한 관측 시퀀스의 확률 P(O

   F)를 어떻게 효율적으로 계산할 수 있을까?

2. Decoding: 관측 시퀀스 O=(o1o2…oT)와 HMM 모델 F = (A,B)가 주어졌을 때, 어떤 의미에서 최적인 상태 시퀀스 Q=(q1q2…qT)를 어떻게 선택할 수 있을까? (즉, 관측값을 가장 잘 설명하는 시퀀스는 무엇인가?)

3. Learning: 모델 파라미터 F = (A,B)를 어떻게 조정해야 P(O

   F)를 최대화할 수 있을까?

Evaluation : Forward Algorithm

emission probablity 를 모든 경우에 대해서 구하려면 많은 경우에 수가 존재한다. 이를 효율적으로 계산하기 위해 Dynamic Programming 을 사용한다.

\[\alpha_t(j) = \sum_{i=1}^{n} \alpha_{t-1}(i) \times a_{ij} \times b_j(o_t)\]

$alpha_t(1)$ , $alpha_t(2)$ 등을 memoization 하여 반복하여 사용

Decoding : Viterbi intuition

가장 효율이 좋은 시퀀스를 뽑는 알고리즘

\[v_t(j) = \max_{i \in \{1, \ldots, n\}} \left[ v_{t-1}(i) \times a_{ij} \times b_j(o_t) \right]\]

Forward Algorithm은 각 상태에서의 α를 구하기 위해 가능한 모든 경우의 수를 고려해 그 확률들을 더해줬다면(sum), 디코딩은 그 확률들 가운데 최대값(max)에 관심이 있다.

비터비 역시 계산 결과를 활용하는 다이내믹 프로그래밍 기법을 쓴다.

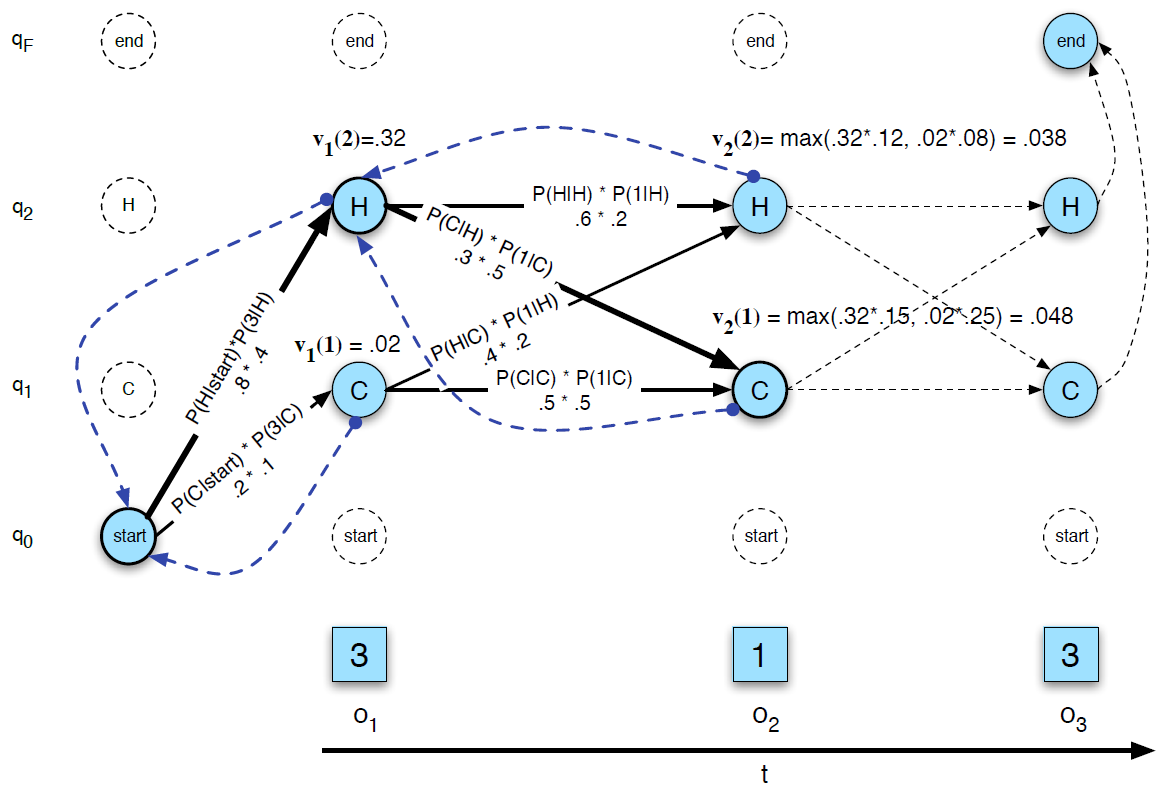
시퀀스를 확인해야 하기 때문에 최대확률을 구한 뒤 backtracking 과정을 거친다. 파란색 선이 backtracking 과정

Learning

전방확률 : 현재 상태의 발생 확률

후방확률 : 현재 상태 이후의 발생확률

\[\alpha_t(j) = \sum_{i=1}^{n} \alpha_{t-1}(i) \times a_{ij} \times b_j(o_t) \beta_t(i) = \sum_{j=1}^{n} a_{ij} \times b_j(o_{t+1}) \times \beta_{t+1}(j)\]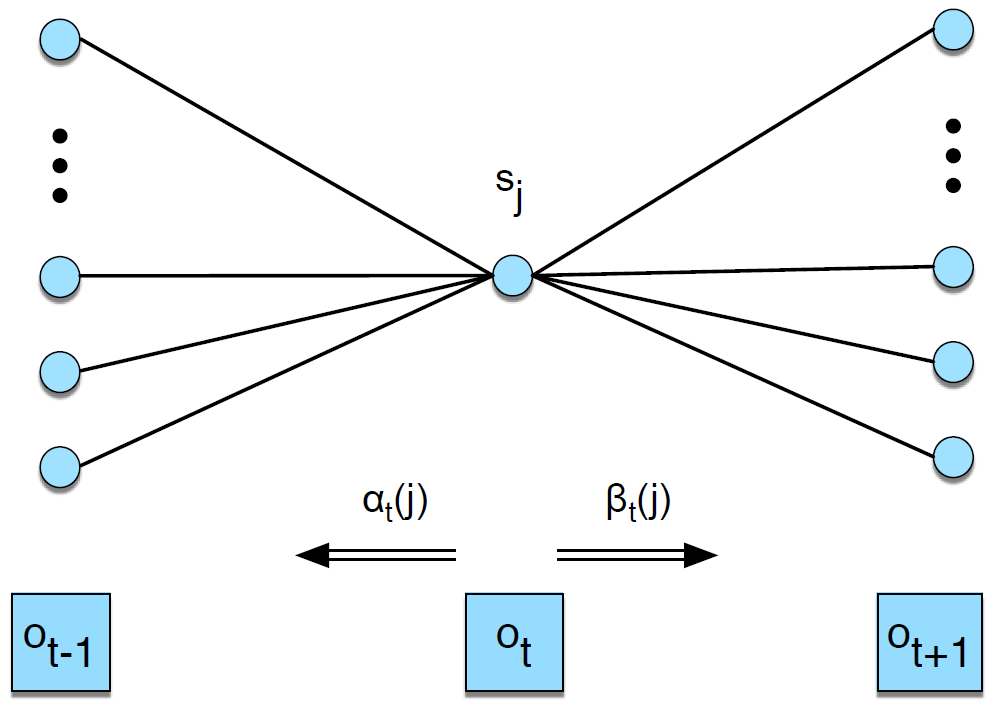

상태의 발생 우도(likelihood) : 전방확률 * 후방확률

\[\alpha_t(j) \times \beta_t(j) = P(q_t = j, \mathbf{O} \mid \lambda)\]

t 번째 시점에 상태 j 일 확률을 의미한다.

Emission Calcualte

시점에 𝑗번째 상태일 확률 γ𝑡(𝑗)

\[\gamma_t(j) = \frac{P(q_t = j, \mathbf{O} \mid \lambda)}{P(\mathbf{O} \mid \lambda)} = \frac{\alpha_t(j) \times \beta_t(j)}{\sum_{s=1}^{n} \alpha_t(s) \times \beta_t(s)}\]

𝑗 번째 상태에서 관측치 𝑣𝑘가 나타날 방출확률

\[\hat{b}_j(v_k) = \frac{\sum_{t=1}^{T} \text{s.t. } o_t = v_k \gamma_t(j)}{\sum_{t=1}^{T} \gamma_t(j)}\]

방출확률 𝑏̂ 𝑗(𝑣𝑘)의 분모는 𝑗 번째 상태가 나타날 확률

분자는 𝑗번째 상태이면서 그 때 관측치(𝑜𝑡)가 𝑣𝑘일 확률

어떤 시점이든 𝑗번째 상태가 나타날 확률 γ가 존재하므로 𝑇개 관측치 시퀀스 전체에 걸쳐 모든 시점에 대해 γ를 더해주는 것

Transition Probability Update And ξ

𝑡 시점에 𝑖 번째 상태이고 𝑡+1 시점에 𝑗 번째 상태일 확률 ξ

\[\xi_t(i, j) = \frac{P(q_t = i, q_{t+1} = j, \mathbf{O} \mid \lambda)}{P(\mathbf{O} \mid \lambda)}\]

전이할 확률

\[\xi_t(i, j) = \frac{P(q_t = i, q_{t+1} = j, \mathbf{O} \mid \lambda)}{P(\mathbf{O} \mid \lambda)} = \frac{\alpha_t(i) \times a_{ij} \times b_j(o_{t+1}) \times \beta_{t+1}(j)}{\sum_{s=1}^{n} \alpha_t(s) \times \beta_t(s)}\]

분모 : 모든 상태가 될 확률

분자 : 특정 상태가 될 확률

\[\hat{a}_{ij} = \frac{\sum_{t=1}^{T-1} \xi_t(i, j)}{\sum_{t=1}^{T-1} \sum_{k=1}^{N} \xi_t(i, k)}\]

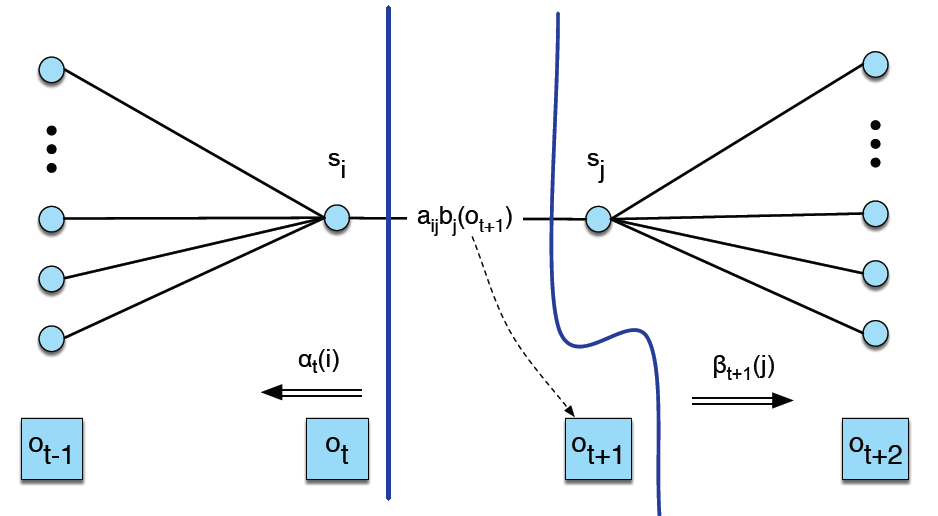
Learning : EM Algorithm

은닉마코프모델의 파라메터는 전이확률(Transition) 𝐴 와 방출확률(Emission) 𝐵

이 두 파라메터를 동시에 추정하기는 어렵다.

예제에서 우리가 관측가능한 것은 아이스크림의 개수뿐, 궁극적으로 알고 싶은 날씨는 숨겨져 있다.

따라서 HOT에서 COLD로 전이할 확률은 물론 날씨가 더울 때 아이스크림을 1개 먹을 방출확률들을 모두 한번에 알 수 없다.

이럴 때 주로 사용되는 것이 EM 알고리즘. HMM에서는 이를 ‘바움-웰치 알고리즘’ 또는 ‘Forward, Backward Algorithm’이라고도 부른다.

E-step

모델 파라메터 λ, 즉 전이확률 𝐴, 방출확률 𝐵 를 고정시킨 상태에서 관측치 𝑂를 바탕으로 전방확률 α 와 후방확률 β를 업데이트. 이 α 와 β 를 바탕으로 γ 와 ξ 를 각각 계산.

M-step

E-step에서 구한 γ 와 ζ를 바탕으로 모델 파라메터 𝐴, 𝐵를 업데이트

Programming

ratsgo’s HMM 참고