None linear model & Kernel Function
Overview
이번 포스팅은 supervised learning(지도 학습)에서 사용되는 데이터 모델인 비선형 모델에 대해서 포스팅합니다. 지도학습의 개념, 회귀 분석의 개념, 데이터 모델의 종류인 선형 모델과 비선형 모델의 차이점에 대해 간단히 정리합니다. 이후 비선형 모델의 회귀 분석 방법인 커널 기법, 서포트 백터 머신(SVM, Support Vector Machine), 의사결정트리의 개념 대해서 정리합니다.
Prerequisite
Supervised learning
지도 학습 (Supervised Learning)은 훈련 데이터(Training Data)로부터 하나의 함수를 유추해내기 위한 기계 학습(Machine Learning)의 한 방법입니다.
훈련 데이터는 일반적으로 입력 객체에 대한 속성을 벡터 형태로 포함하고 있으며 각각의 벡터에 대해 원하는 결과가 무엇인지 표시됩니다. 이 데이터를 통해 유추한 인과관계를 연속된 함수로써 나타내는것을 회귀분석(Regression)이라 하고 주어진 입력 벡터가 어떤 종류의 값인지 표식하는 것을 분류(Classification)라 합니다.
지도 학습기(Supervised Learner)가 하는 작업은 훈련 데이터로부터 주어진 데이터에 대해 예측하고자 하는 값을 올바로 추측해내는 것입니다.
이 목표를 달성하기 위해서는 학습기가 알맞은 방법을 통하여 기존의 훈련 데이터로부터 나타나지 않던 상황까지도 일반화하여 처리할 수 있어야 합니다.
Regression Analysis
독립변수와 종속변수의 인과 관계를 파악하기 위한 분석입니다. 대표적인 용례는 마케팅에서 다음과 같이 광고료와 총판매량의 인과관계를 파악하는 경우리 할 수 있습니다. 독립변수 X라 두고 결과값을 총판매량 종속변수 Y로 둔 원본 데이터 입니다.
| 상점번호 | 광고료 X | 총판매량 Y | |———-|———-|———-| | 1 | 4 | 9 | | 2 | 8 | 20 | | 3 | 9 | 22 | | 4 | 8 | 15 | | 5 | 8 | 17 | …
아래는 위 표를 산점도로 나태낸 것입니다.
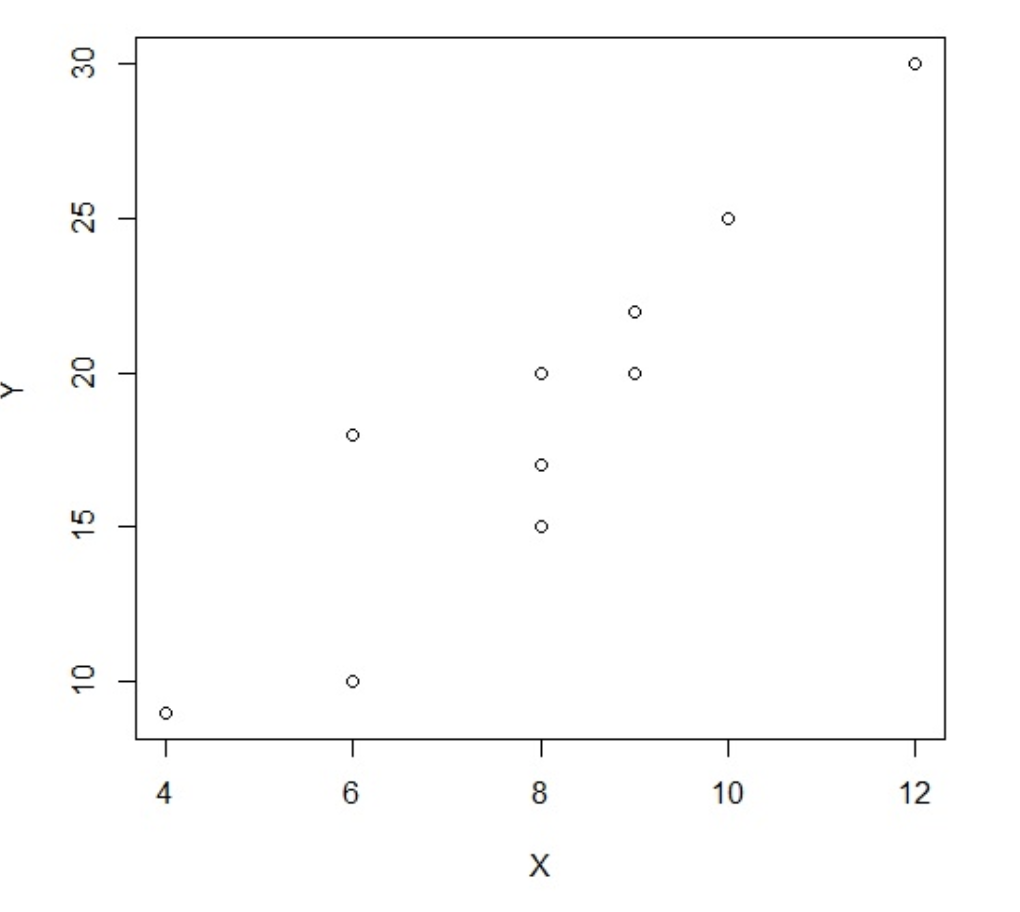
눈으로 봤을 때, 대충 광고료 X가 올라갈때마다 총판매량 Y가 증가하는 것을 볼 수 있습니다. 그 관계가 대충 직선(y = ax + b)이라는 것도 알 수 있습니다. 즉 광고료와 총판매량이 어느정도 인과 관계를 갖는 것을 확인 할 수 있습니다.
이렇게 독립변수와 종속변수간의 인과 관계를 통계적으로 파악하는 과정을 회귀분석이라 합니다.
인과분석이 아닌 회귀분석이라 하는지는 회귀분석의 기원에 따릅니다.
최초 아버지와 자식의 키의 인과관계라는 주제로 회귀분석을 시도 했던 Francis Galton의 분석 결과가
아들의 키는 그 세대의 전체 평균의 키로 회귀한다라는 결과를 냈기 때문에 회귀분석으로 명명되었습니다.
Regression Linear model & Nonlinear model
회귀모델을 공부하지 않고 간단하게 선형 회귀 모델에 대해 생각해보면 대부분 의미를 독립 변수(x)와 종속 변수(y) 간의 관계가 일차식으로 표현되는 것이라고 생각할 수 있습니다. 그래서 독립 변수를 제곱근이나 로그 함수 등을 이용해서 적당히 변환하면 비선형 모델을 선형 모델로 만들 수 있다고 생각합니다.
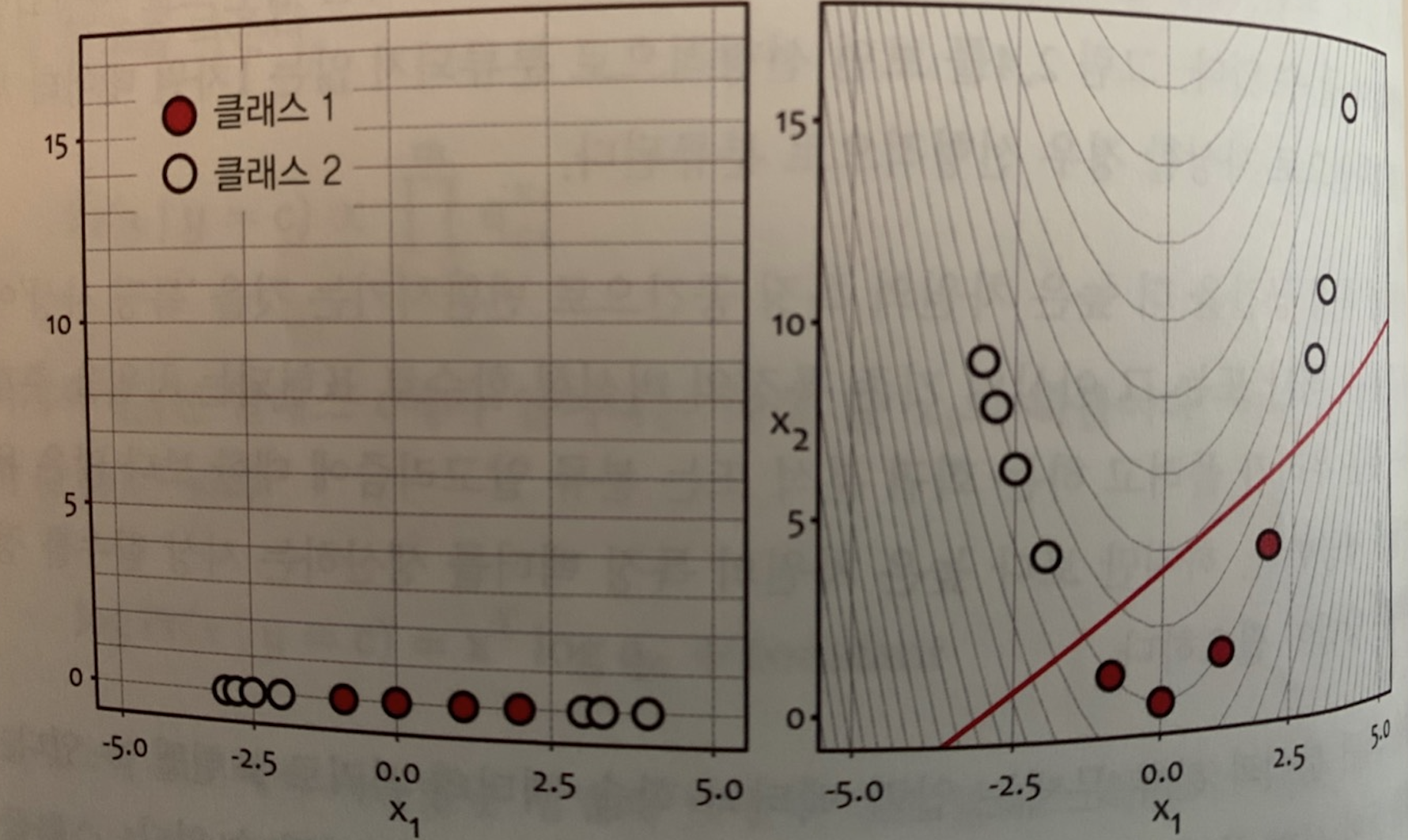
그렇기 때문에 아래 그림에서 왼쪽 그림은 선형 모델이고 오른쪽 그림은 비선형 모델이라고 생각할 수 있습니다.
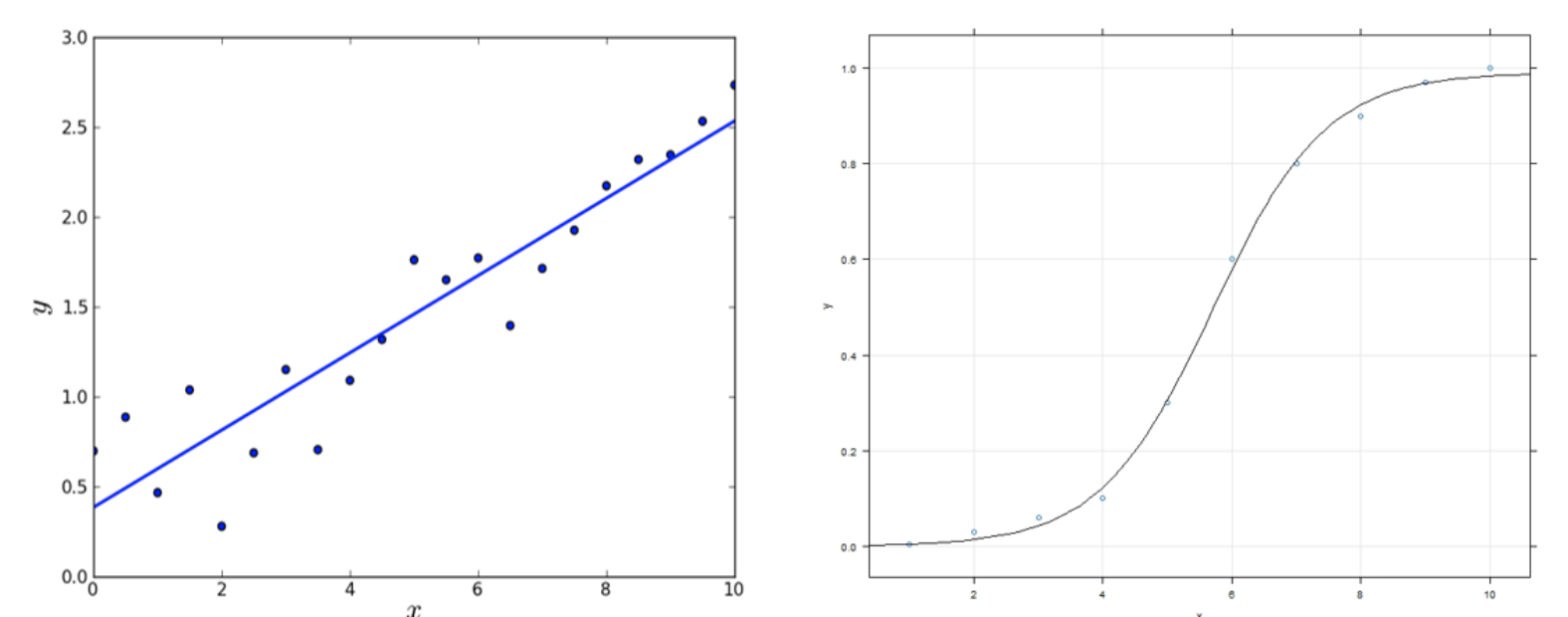
선형 회귀 모델은 회귀 계수(regression coefficient)를 선형 결합으로 표현할 수 있는 모델을 말합니다. 즉, 독립 변수가 일차식이냐 이차식이냐 로그 함수식이냐가 아니라 우리가 추정할 대상인 파라미터가 어떻게 생겼느냐의 문제입니다. 그렇기 때문에 아래 함수들은 모두 선형 회귀식입니다.
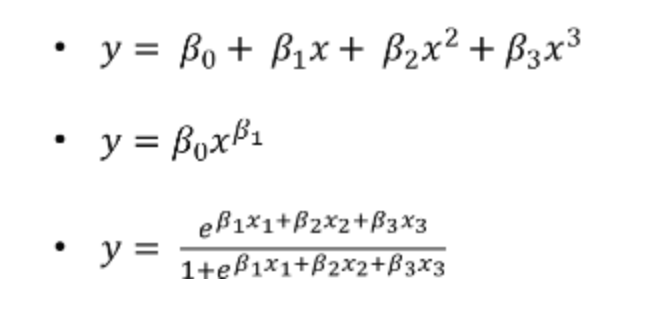
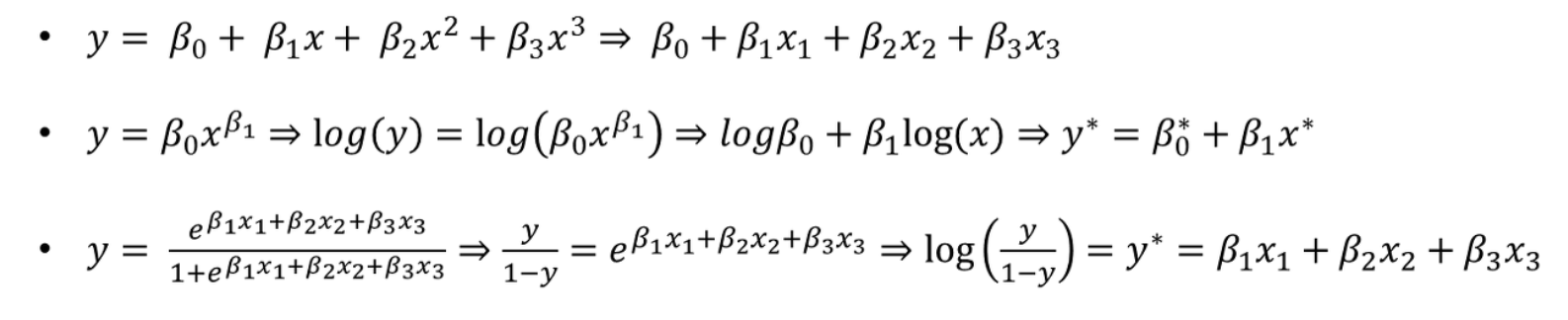
반대로 아래와같은 회귀함수는 비선형 모델이라고 할 수 있습니다.
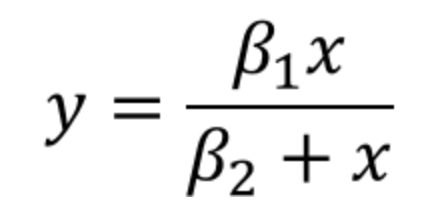
Kernel Trick
동영상.
저차원 공간에서 선형 분리 안되는 데이터들을 고차원 공간에 매핑시켜서 선형 분리되도록 할 수가 있습니다. 이러한 방식을 커널 트릭이라 합니다. 커널 트릭을 위해서는 저차원->고차원 매핑 함수가 필요합니다. 예를 들어, a=(0,0), b=(1,1) 이라는 2차원 점들이 있다고 하고. 이를 3차원 공간으로 매핑시키기 위해서, M(x) = (x1^2, 루트2 * x1*x2, x2^2) 라는 매핑함수를 정의합니다. 그러면 a=(0,0) –> a=(0,0,0) b=(0,0,0) –> b=(1, 루트2, 1) 라는 3차원 공간 좌표로 맵핑됩니다. 여기서 M(x): L -> H (저차원에서 고차원으로 매핑시켜주는 매핑 함수) 가 됩니다. 이 상태에서 커널 함수의 정의를 살펴보면, . L (저차원) 공간 상의 두 벡터 x, y 가 있다고 할 때, 커널 함수 K(x, y) = M(x) * M(y) 를 만족하는 매핑함수 M(.) 가 존재해야 한다. 즉, 커널 함수의 값과 H 공간 상으로 매핑된 두점 M(x), M(y) 의 내적이 같아야 한다.
즉, 여기서 말하는 커널 함수란 K(x, y) = M(x) * M(y) 를 만족하는 매핑함수가 존재할 때. K 를 말합니다.
위와 같은 형태의 커널 함수 종류는 다음과 같습니다.
- 다항식 커널
- RBF (Radial Basis Function) 커널
- 하이퍼볼릭 탄젠트 커널
SVM
Support Vector Machine(SVM)은 커널 트릭을 이용한 분석 방법입니다. 원 훈련(또는 학습)데이터를 비선형 매핑(Mapping)을 통해 고차원으로 변환합니다. 이 새로운 차원에서 초평면(hyperplane)을 최적으로 분리하는 선형분리를 찾습니다. 즉, 최적의 Decision Boundary(의사결정 영역)를 찾는 방식입니다.
SVM은 복잡한 비선형 의사결정 영역을 모형화 할 수 있기 때문에 매우 정확하며, 다른 모델들 보다 Over Fitting되는 경향이 적다고합니다.
"""
==============
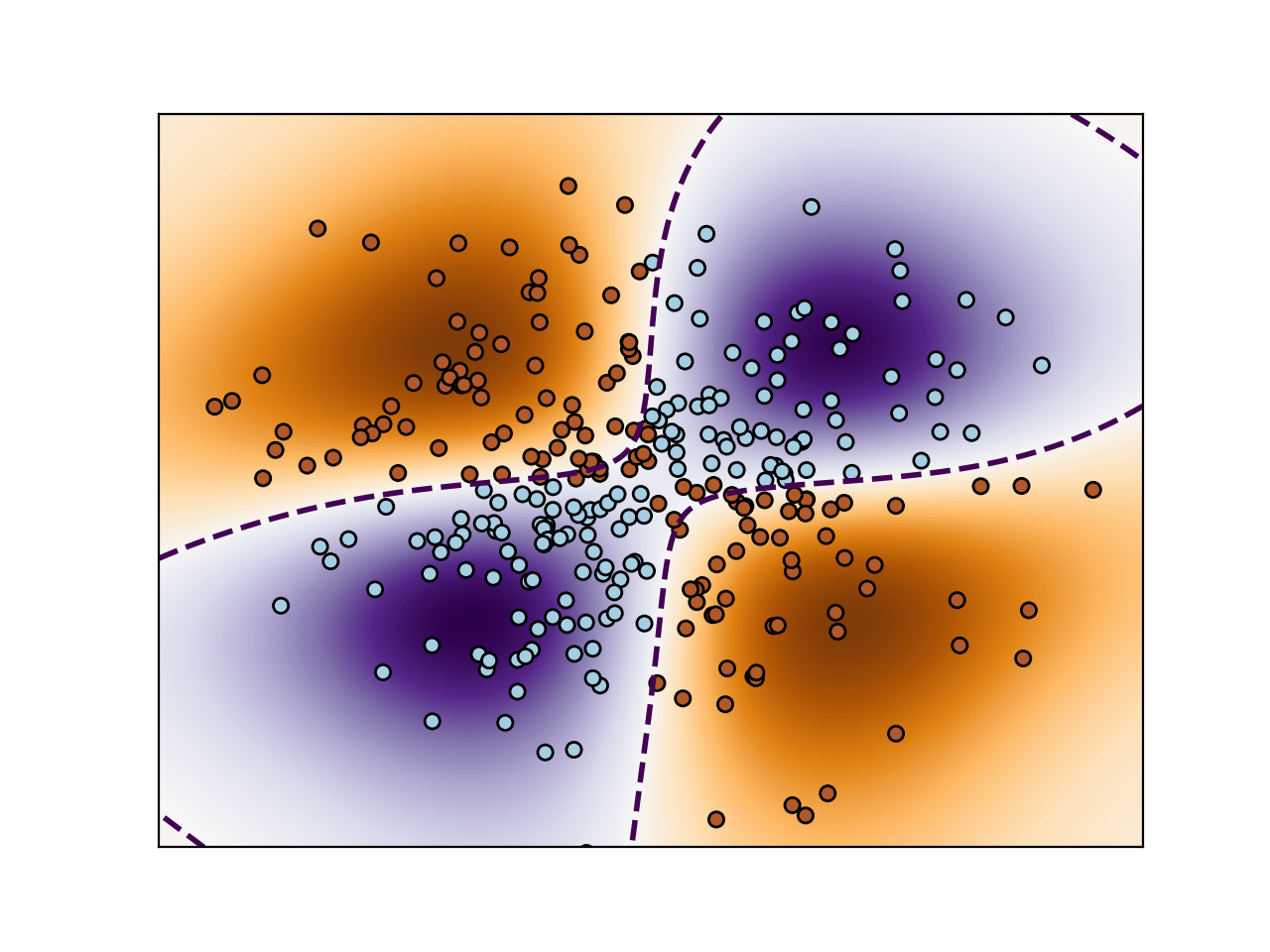
Non-linear SVM
==============
Perform binary classification using non-linear SVC
with RBF kernel. The target to predict is a XOR of the
inputs.
The color map illustrates the decision function learned by the SVC.
"""
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
xx, yy = np.meshgrid(np.linspace(-3, 3, 500),
np.linspace(-3, 3, 500))
np.random.seed(0)
X = np.random.randn(300, 2)
Y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
# fit the model
clf = svm.NuSVC(gamma='auto')
clf.fit(X, Y)
# plot the decision function for each datapoint on the grid
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.imshow(Z, interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()), aspect='auto',
origin='lower', cmap=plt.cm.PuOr_r)
contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2,
linestyles='dashed')
plt.scatter(X[:, 0], X[:, 1], s=30, c=Y, cmap=plt.cm.Paired,
edgecolors='k')
plt.xticks(())
plt.yticks(())
plt.axis([-3, 3, -3, 3])
plt.show()
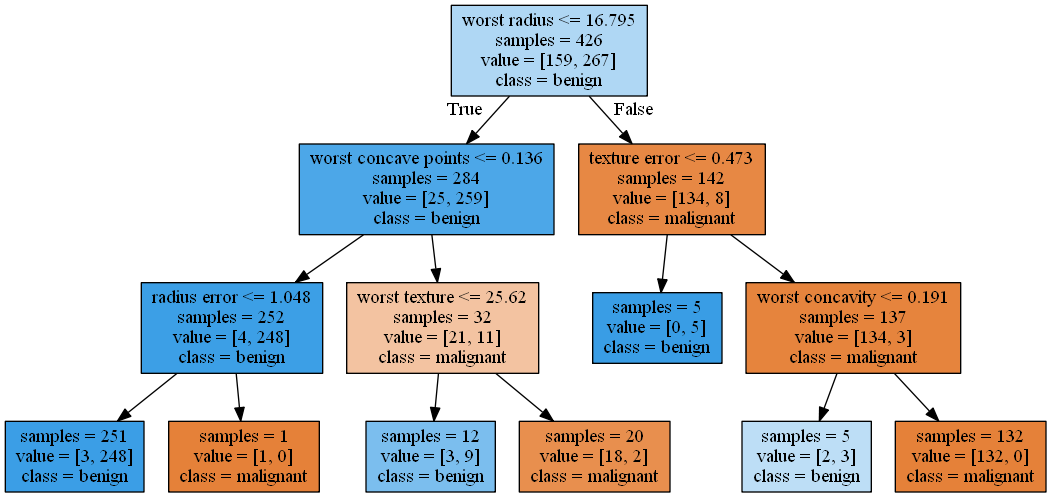
Decision Tree
의사결정 규칙(rule)을 나무구조로 도표화하여 분류(classification)와 예측(prediction)을 수행하는 분석방법입니다. 이 방법은 분류 또는 예측이 나무구조에 의한 추론규칙(induction rule)에 의해서 표현되기 때문에 다른 방법들(예, 신경망분석, 판별분석, 회귀분석 등)에 비해 그 과정을 쉽게 이해하고 설명할 수 있습니다.
의사결정나무의 형성과정
- 이산형 변수의 경우
- 카이제곱 통계량의 p-값 (p-value of Chi Square statistic)
- 지니 지수(Gini index)
- 엔트로피 지수(Entropy index)
- 연속형 변수의 경우
- 평균과 표준편차를 이용하여 분리
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.datasets import load_breast_cancer
from sklearn.cross_validation import train_test_split
#Dot to png
import pydot
#온라인 시각화
#https://dreampuf.github.io/GraphvizOnline
#샘플 데이터 로드(유방암 데이터 세트)
cancer = load_breast_cancer()
#훈련, 테스트 데이터 셔플
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
#의사결정 트리 선언
dTreeAll = DecisionTreeClassifier(random_state=0)
#훈련 (모든 리프 노드 사용)
dTreeAll.fit(X_train, y_train)
#점수 출력
print("Train Set Score1 : {:.2f}".format(dTreeAll.score(X_train, y_train)))
print("Test Set Score1 : {:.2f}".format(dTreeAll.score(X_test, y_test)))
#의사결정 트리 선언(트리 깊이 제한)
dTreeLimit = DecisionTreeClassifier(max_depth=3, random_state=0)
#훈련 (가지치기 : 리프노드 깊이 제한)
dTreeLimit.fit(X_train, y_train)
#점수 출력
print("Train Set Score2 : {:.2f}".format(dTreeLimit.score(X_train, y_train)))
print("Test Set Score2 : {:.2f}".format(dTreeLimit.score(X_test, y_test)))
export_graphviz(dTreeLimit, out_file="dicisionTree1.dot", class_names=["malignant","benign"],
feature_names=cancer.feature_names, impurity=False, filled=True)
#Encoding 중요
(graph,) = pydot.graph_from_dot_file('dicisionTree1.dot', encoding='utf8')
#Dot 파일을 Png 이미지로 저장
graph.write_png('dicisionTree1.png')
reference
https://ko.wikipedia.org/wiki/%EC%A7%80%EB%8F%84_%ED%95%99%EC%8A%B5
https://blog.naver.com/PostView.nhn?blogId=vnf3751&logNo=220831047843&proxyReferer=https%3A%2F%2Fwww.google.com%2F
https://scikit-learn.org/stable/modules/svm.html
https://excelsior-cjh.tistory.com/66


Comments